Cara Mengerjakan Limit Tak Tentu
Cara Mengerjakan Limit Tak Hingga Trigonometri Akar
Limit tak hingga adalah salah satu topik yang sering ditemui dalam matematika, terutama dalam trigonometri akar. Pada artikel ini, kami akan membahas cara mengerjakan limit tak hingga trigonometri akar dengan langkah-langkah yang jelas dan mudah dipahami. Kami akan memberikan contoh soal yang sering muncul dan memberikan tips berguna untuk mengatasi kesulitan dalam mengerjakan limit tak hingga.
Contoh Soal Limit Fungsi Aljabar Tak Terhingga
Sebagai permulaan, mari kita lihat contoh soal limit fungsi aljabar tak terhingga. Soal ini seringkali muncul dalam ujian matematika dan bisa menjadi tantangan bagi banyak siswa. Berikut adalah contoh soalnya:
Pertanyaan:
Hitung limit berikut ini:
Jawaban:
Langkah pertama dalam mengerjakan limit ini adalah dengan mengamati fungsi aljabar yang terdapat dalam soal. Dalam contoh soal ini, kita memiliki pecahan matematika dengan pangkat tertinggi pada pembilang dan penyebut adalah x^3. Jadi, kita dapat menggunakan aturan pangkat tertinggi pada limit tak hingga.
Jika kita memiliki fungsi aljabar tak terhingga dengan pangkat tertinggi pada pembilang dan penyebut adalah x^n, maka kita dapat membuat keputusan mengenai limit tersebut berdasarkan pangkat tertinggi tersebut:
- Jika n > 1, maka limit tak hingga tersebut sama dengan tak terhingga.
- Jika n < 1, maka limit tak hingga tersebut mendekati 0.
- Jika n = 1, maka kita perlu melakukan langkah-langkah lebih lanjut untuk menentukan limit tak hingga tersebut.
Kembali ke contoh soal di atas. Kita memiliki x^3 sebagai pangkat tertinggi pada pembilang dan penyebut. Karena pangkat tertinggi tersebut lebih besar dari 1, kita dapat menyimpulkan bahwa limit tersebut adalah tak terhingga. Oleh karena itu, hasil limit dari soal tersebut adalah tak terhingga.
Dalam kasus lain, jika kita memiliki n = 1 dalam fungsi aljabar tak terhingga, maka kita perlu menerapkan langkah-langkah tambahan untuk menentukan limit tersebut. Mari kita lihat contoh soal berikut ini:
Pertanyaan:
Hitung limit berikut ini:
Jawaban:
Pada contoh soal ini, kita memiliki limit tak hingga dengan n = 1. Oleh karena itu, kita perlu membagi pembilang dan penyebut dengan pangkat tertinggi dari x, yaitu x. Setelah itu, kita dapat menyederhanakan persamaan tersebut:
Setelah kita menyederhanakan persamaan tersebut, kita dapat melihat bahwa limit dari soal tersebut adalah 2. Jadi, itu adalah hasil yang benar untuk limit tak hingga dengan n = 1 pada fungsi aljabar tak terhingga.
Cara Mengerjakan Limit Tak Hingga Trigonometri Akar
Selanjutnya, mari kita bahas cara mengerjakan limit tak hingga trigonometri akar. Limit tak hingga trigonometri seringkali melibatkan fungsi sinus, kosinus, atau tangen. Sebelum kita memahami langkah-langkah untuk mengerjakan limit tak hingga trigonometri akar, ada baiknya kita memahami beberapa properti trigonometri terlebih dahulu.
Properti trigonometri yang akan kita bahas dalam konteks limit tak hingga adalah properti sudut istimewa pada segitiga siku-siku. Sudut-sudut istimewa tersebut adalah 30°, 45°, dan 60°.
Dalam konteks limit tak hingga trigonometri akar, kita perlu mengingat bahwa nilai sinus sudut-sudut istimewa tersebut adalah:
- sin(30°) = 1/2
- sin(45°) = √2/2
- sin(60°) = √3/2
Selain itu, kita juga perlu mengingat nilai kosinus sudut-sudut istimewa tersebut:
- cos(30°) = √3/2
- cos(45°) = √2/2
- cos(60°) = 1/2
Dengan memahami properti sudut istimewa ini, kita dapat lebih mudah dalam mengerjakan limit tak hingga trigonometri akar.
Untuk memahami langkah-langkah yang kami jelaskan di bawah ini, mari kita lihat contoh soal berikut ini:
Pertanyaan:
Hitung limit berikut ini:
Jawaban:
Langkah pertama dalam mengerjakan limit tak hingga trigonometri akar adalah dengan mengamati fungsi trigonometri yang terdapat dalam soal. Pada contoh soal di atas, kita memiliki persamaan akar dari sinus kuadrat x.
Langkah kedua adalah mencoba menyederhanakan persamaan tersebut menggunakan properti sudut istimewa yang telah kita bahas sebelumnya. Dalam persamaan ini, kita dapat menggunakan properti sudut istimewa sin(30°) = 1/2.
Setelah itu, kita dapat menyederhanakan persamaan tersebut menjadi:
Langkah berikutnya adalah menghitung limit dari persamaan di atas. Karena kita memiliki akar kuadrat pada limit tersebut, kita dapat menghilangkan akar kuadrat dengan mengkuadratkan persamaan tersebut.
Setelah kita mengkuadratkan persamaan tersebut, kita dapat menyederhanakan limit menjadi:
Setelah kita menyederhanakan limit menjadi bentuk ini, kita dapat melihat bahwa hasil limit tersebut adalah 1/4. Jadi, itu adalah hasil yang benar untuk limit tak hingga trigonometri akar pada contoh soal tersebut.
Dalam beberapa kasus, mengerjakan limit tak hingga trigonometri akar bisa menjadi lebih rumit dan membutuhkan beberapa langkah tambahan. Namun, dengan memahami properti sudut istimewa dan mengikuti langkah-langkah yang telah dijelaskan di atas, Anda dapat dengan mudah mengerjakan limit tak hingga trigonometri akar.
Tips
Untuk membantu Anda lebih baik dalam mengerjakan limit tak hingga trigonometri akar, berikut adalah beberapa tips yang mungkin bermanfaat:
- Periksa kembali aturan pangkat tertinggi pada limit tak hingga untuk fungsi aljabar tak terhingga.
- Pelajari dan hafalkan properti sudut istimewa pada segitiga siku-siku untuk memudahkan dalam mengerjakan limit tak hingga trigonometri akar.
- Gunakan properti sudut istimewa tersebut untuk menyederhanakan persamaan trigonometri sebelum menghitung limit.
- Amati secara seksama persamaan limit dan cari pola-pola yang dapat membantu dalam menyederhanakan limit tersebut.
- Latihanlah dengan banyak contoh soal untuk meningkatkan pemahaman Anda dalam mengerjakan limit tak hingga trigonometri akar.
Dengan mengikuti tips di atas dan berlatih secara teratur, Anda akan semakin mahir dalam mengerjakan limit tak hingga trigonometri akar.
Kesimpulan
Dalam artikel ini, kita telah membahas cara mengerjakan limit tak hingga trigonometri akar dengan langkah-langkah yang jelas dan mudah dipahami. Kami telah memberikan contoh soal yang sering muncul dan menjelaskan cara menyederhanakan persamaan trigonometri menggunakan properti sudut istimewa. Kami juga memberikan tips berguna yang dapat membantu Anda dalam mengerjakan limit tak hingga trigonometri akar dengan lebih baik.
Semoga artikel ini bermanfaat dan membantu Anda dalam memahami cara mengerjakan limit tak hingga trigonometri akar. Selamat belajar dan semoga sukses!
(Nah|Begitulah|Itulah|Sekian|Ok)(pembahasan|materi|info|artikel|postingan)(tentang|mengenai) Cara Mengerjakan Limit Tak Tentu. (Apabila|Jika|Kalau) (kurang|belum|tidak) (faham|jelas) atau (untuk|sebagai) (info|materi) (pelengkap|tambahan), (dibawah|dibawah ini|silahkan) ada beberapa gambar terkait tentang Cara Mengerjakan Limit Tak Tentu. Silahkan baca dibawah ini:
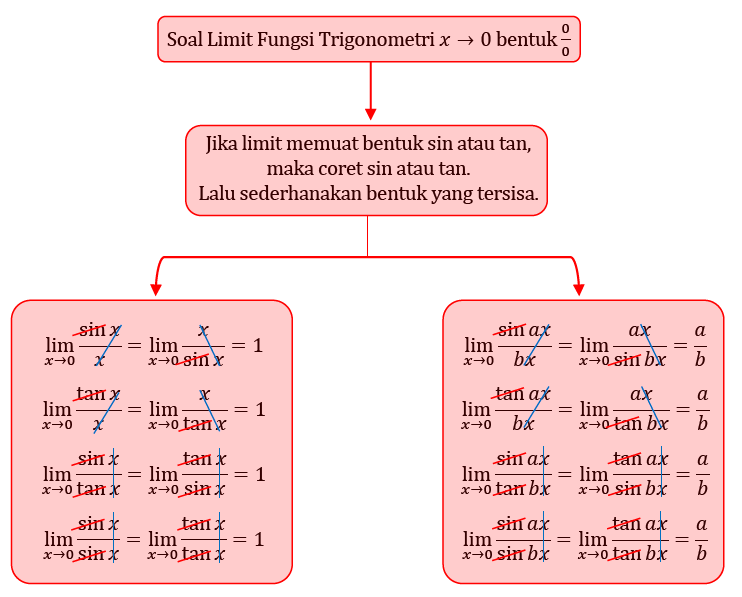
Contoh Soal Limit Fungsi Trigonometri Bentuk Pecahan
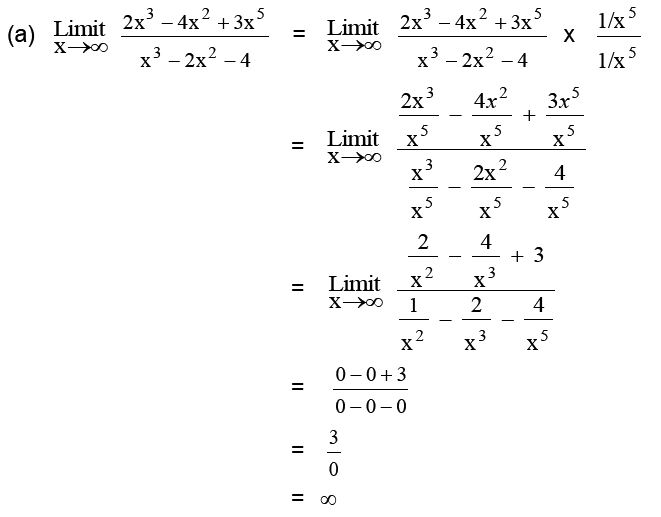Sumber gambar : contoh123.com Cara Mengerjakan Limit Tak Hingga Trigonometri Akar - Fasrtastic
Sumber gambar : fasrtastic970.weebly.com Cara Mengerjakan Limit Tak Hingga Trigonometri Akarcraft - Olporbh
Sumber gambar : olporbh.weebly.com Contoh Soal Limit Tak Tentu
Sumber gambar : www.ainamulyana.my.id Contoh Soal Limit Fungsi Aljabar Tak Terhingga – Kumpulan Contoh Surat
Sumber gambar : contohterbaru.com Cara Mengerjakan Limit Tak Hingga Trigonometri Akarcraft - Passabites
Sumber gambar : passabites.weebly.com Cara Menghitung Limit Tak Hingga - Dunia Sosial
Sumber gambar : duniasosial.com Cara Mengerjakan Soal Limit Tak Tentu Nol Per Nol | KING OF SCIENCE
Sumber gambar : jeffreyphysics.blogspot.com tentu nol mengerjakan
Contoh Soal Limit Fungsi Aljabar Dengan Cara Substitusi - Bakti Soal
Sumber gambar : baktisoal.blogspot.com fungsi aljabar mengerjakan tentu matematika kompasiana rasional substitusi koin pelemparan sampel
Cara menghitung limit tak hingga. Cara mengerjakan limit tak hingga trigonometri akar. Cara mengerjakan limit tak hingga trigonometri akarcraft. Tentu nol mengerjakan. Contoh soal limit fungsi aljabar dengan cara substitusi. Cara mengerjakan limit tak hingga trigonometri akarcraft. Cara mengerjakan soal limit tak tentu nol per nol. Fungsi aljabar mengerjakan tentu matematika kompasiana rasional substitusi koin pelemparan sampel. Contoh soal limit fungsi aljabar tak terhingga – kumpulan contoh surat